受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)是G.Hinton教授的一宝。Hinton教授是深度学习的开山鼻祖,也正是他在2006年的关于深度信念网络DBN的工作,以及逐层预训练的训练方法,开启了深度学习的序章。其中,DBN中在层间的预训练就采用了RBM算法模型。RBM是一种无向图模型,也是一种神经网络模型。
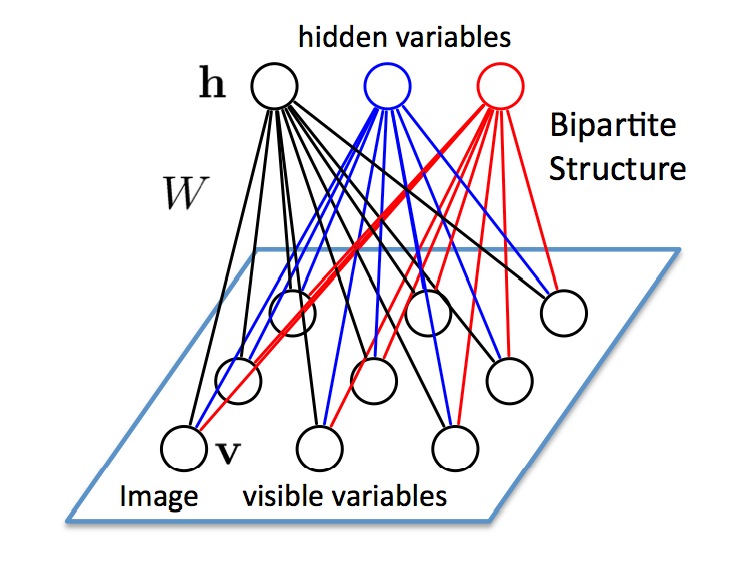
RBM具有两层:可见层(V层),以及隐藏层(H层)。可以看到,两层神经元之间都是全连接的,但是每一层各自的神经元之间并没有连接,也就是说,RBM的图结构是一种二分图(bipartite graph)。正是这个特点,才叫受限玻尔兹曼机,玻尔兹曼机是允许同一层之间的神经元相连的。RBM其实是一种简化了的BM模型。
还有一个特点,RBM中的神经元都是二值化的,也就是说只有激活和不激活两种状态,也就是0或者1;可见层和隐藏层之间的边的权重可以用$W$来表示,$W$是一个$|V|×|H|$大小的实数矩阵。算法难点主要就是对$W$求导(当然还有bias参数),用于梯度下降的更新;但是因为$V$和$H$都是二值化的,没有连续的可导函数去计算,实际中采用的sampling的方法来计算,这里面就可以用比如Gibbs sampling的方法,当然,Hinton提出了对比散度DC方法,比Gibbs方法更快,已经成为求解RBM的标准解法。
RBM模型结构
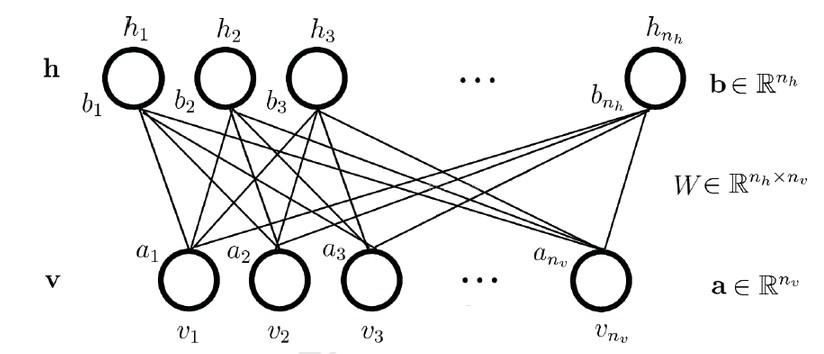
因为RBM隐层和可见层是全连接的,为了描述清楚与容易理解,把每一层的神经元展平即可,见下图[7],本文后面所有的推导都采用下图中的标记来表示。
再重提一下,经典的RBM模型中的神经元都是binary的,也就是说上面图中的神经元取值都是$(0,1) $的。实际上RBM也可以做实数性的model,不过这一块可以先放一放,先来看binary的基本model。
RBM能量函数
RBM是一个能量模型(Energy based model, EBM),是从物理学能量模型中演变而来;能量模型需要做的事情就是先定义一个合适的能量函数,然后基于这个能量函数得到变量的概率分布,最后基于概率分布去求解一个目标函数(如最大似然)。RBM的过程如下:
我们现在有的变量是$(v,h)$,包括隐层和可见层神经元;参数包括$θ=(W,a,b)$。能量函数定义:
$$ E_θ(v,h)=−∑_{i=1}^{n_v}a_iv_i−∑_{j=1}^{n_h}b_jh_j−∑_{i=1}^{n_v}∑_{j=1}^{n_h}h_jw_{j,i}v_i$$
如果写成向量/矩阵的形式,则为:
$$E_θ(v,h)=−a^Tv−b^Th−h^TWv$$
那么,可以得到变量$(v,h)$的联合概率分布是:
$$P_θ(v,h)=\frac {1}{Z_θ}e^{−E_θ(v,h)}$$
其中,$Z_θ$称为归一化因子,作用是使得概率之和(或者积分)为1,形式为:
$$Z_θ=∑_{v,h}e^{−E_θ(v,h)}$$
在上面所有算式中,下标$θ$都表示在参数$θ=(W,a,b)$下的表达,为了书写的简洁性,本文余下部分如果没有特殊指定说明,就省略下标$θ$了,但含义不变。
当我们有了联合概率分布,如果想求观察数据(可见层)的概率分布$P(v)$,则求边缘分布:
$$P(v)=∑_hP(v,h)=\frac1Z∑_he^{−E(v,h)}$$
相对应的,如果想求隐层单元的概率分布$P(h)$,则求边缘分布:
$$P(h)=∑_vP(v,h)=\frac1Z∑_ve^{−E(v,h)}$$
当然,我们不太可能直接计算$Z$,因为$Z$的求和中存在指数项种可能——$2^{n_v+n_h}$种取值。接下来考虑条件概率,即可见层神经元状态给定时,(任意)隐藏层神经元状态为1的概率,即$P(h_k=1|v)$。类似的也可以求$P(v_k=1|h)$,方法也是差不多的,下面就只对$P(h_k=1|v)$进行描述。我们可以推导出:
$$P(h_k=1|v)=sigmoid(b_k+∑_{j=1}^{n_v}w_{kj}v_j)$$
以及
$$P(v_k=1|h)=sigmoid(b_k+∑_{j=1}^{n_v}w_{kj}h_j)$$
可以直接知道结果即可,证明可以跳过。这里我们可以看到,sigmoid是一种激励函数,因此才把RBM也叫做一种神经网络模型。
证:以下记$h_{−k}$表示隐藏层神经元k以外的神经元。
$$P(h_k=1|v)=P(h_k=1|h_{−k},v)$$
$$=\frac {P(h_k=1,h_{−k},v)}{P(h_{−k},v))}$$
$$=\frac {P(h_k=1,h_{−k},v)}{P(h_k=1,h_{−k},v))+P(h_k=0,h_{−k},v))}$$
$$=\frac{\frac1Ze^{−E(h_k=1,h_{−k},v)}}{\frac1Ze^{−E(h_k=1,h_{−k},v))}+\frac 1Ze^{−E(h_k=0,h_{−k},v))}}$$
$$=\frac1{1+e^{−E(h_k=0,h_{−k},v))+E(h_k=1,h_{−k},v)}}$$
$$=\frac 1{1+e^{−(b_k+∑^{n_v}_{j=1}w_{kj}v_j)}}$$
$$=sigmoid(b_k+∑_{j=1}^{n_v}w_{kj}v_j)$$
因为假设同层神经元之间相互独立,所以有:
$$P(h|v)=∏_{j=1}^{n_h}P(h_j|v)$$
$$P(v|h)=∏_{i=1}^{n_v}P(v_i|h)$$
RBM目标函数
假设给定的训练集合是$S=\{v^i\}$,总数是$n_s$,其中每个样本表示为$v^i=(v^i_1,v^i_2,…,v^i_{n_v})$,且都是独立同分布i.i.d的。RBM采用最大似然估计,即最大化
$$\ln L_S=\ln ∏_{i=1}^{n_s}P(v^i)=∑_{i=1}^{n_s}\ln P(v^i)$$
参数表示为$θ=(W,a,b)$,因此统一的参数更新表达式为:
$$θ=θ+η\frac{∂\ln LS}{∂θ}$$
其中,$η$表示学习速率。因此,很明显,只要我们可以求解出参数的梯度,我们就可以求解RMB模型了。我们先考虑任意单个训练样本$(v^0)$的情况,即
$$L_S=\ln P(v^0)=\ln (\frac1Z∑_he^{−E(v^0,h)})$$
$$=\ln∑_he^{−E(v^0,h)}−\ln∑_{v,h}e^{−E(v,h)}$$
其中$v$表示任意的训练样本,而$v^0$则表示一个特定的样本。
$$\frac {∂L_S}{∂θ}=\frac {∂\ln P(v^0)}{∂θ}$$
$$=\frac ∂{∂θ}(\ln ∑_he^{−E(v^0,h)})−\frac ∂{∂θ}(\ln∑_{v,h}e^{−E(v,h)})$$
$$=−\frac1{∑_he^{−E(v^0,h)}}∑_he^{−E(v^0,h)}\frac {∂E(v^0,h)}{∂θ}+\frac 1{∑_{v,h}e^{−E(v,h)}}∑_{v,h}e^{−E(v,h)}\frac {∂E(v,h)}{∂θ}$$
$$=−∑_hP(h|v^0)\frac {∂E(v^0,h)}{∂θ}+∑_{v,h}P(h,v)\frac {∂E(v,h)}{∂θ}$$
(其中第3个等式左边内条件概率$P(h|v^0)$,因为$\frac {e^−E(v^0,h)}{∑_he^{−E(v^0,h)}}=\frac {e^{−E(v^0,h)}/Z}{∑_he^{−E(v^0,h)}/Z}=\frac{P(v^0,h)}{P(v^0)}=P(h|v^0)$)
上面式子的两个部分的含义是期望——左边是梯度$\frac{∂E(v0,h)}{∂θ}$在条件概率分布$P(h|v^0)$下的期望;右边是梯度$\frac {∂E(v,h)}{∂θ}$在联合概率分布$P(h,v)$下的期望。要求前面的条件概率是比较容易一些的,而要求后面的联合概率分布是非常困难的,因为它包含了归一化因子$Z$(对所有可能的取值求和,连续的情况下是积分),因此我们采用一些随机采样来近似求解。把上面式子再推导一步,可以得到,
$$\frac{∂L_S}{∂θ}=−∑_hP(h|v^0)\frac{∂E(v^0,h)}{∂θ}+∑_vP(v)∑_hP(h|v)\frac{∂E(v,h)}{∂θ}$$
因此,我们重点就是需要就算$∑_hP(h|v)\frac{∂E(v,h)}{∂θ}$,特别的,针对参数$W$,$a$,$b$来说,有
$$∑_hP(h|v)\frac {∂E(v,h)}{∂w_{ij}}=−∑_hP(h|v)h_iv_j$$
$$=−∑_hP(h_i|v)P(h_{−i}|v)h_iv_j$$
$$=−∑_{h_i}P(h_i|v)∑_{h_−i}P(h_{−i}|v)h_iv_j$$
$$=−∑_{h_i}P(h_i|v)h_iv_j$$
$$=−(P(h_i=1|v)⋅1⋅v_j+P(h_i=0|v)⋅0⋅v_j)$$
$$=−P(h_i=1|v)v_j$$
类似的,我们可以很容易得到:
$$\sum _hP(h|v)\frac{∂E(v,h)}{∂a_i}=−v_i$$
$$∑_hP(h|v)\frac{∂E(v,h)}{∂b_j}=−P(h_i=1|v)$$
于是,我们很容易得到,
$$\frac {∂\ln P(v^0)}{∂w_{ij}}=−∑_hP(h|v^0)\frac {∂E(v^0,h)}{∂w_{ij}}+∑_vP(v)∑_hP(h|v)\frac {∂E(v,h)}{∂w_{ij}}$$
$$=P(h_i=1|v^0)v^0_j−∑_vP(v)P(h_i=1|v)v_j$$
$$\frac{∂\ln P(v^0)}{∂a_i}=v^0_i−∑_vP(v)v_i$$
$$\frac {∂\ln P(v^0)}{∂b_i}=P(h_i=1|v^0)−∑_vP(v)P(h_i=1|v)$$
上面求出了一个样本的梯度,对于$n_s$个样本有
$$\frac {∂L_S}{∂w_{ij}}=\sum _{m=1}^{n_s}[P(h_i=1|v^m)v^m_j−∑_vP(v)P(h_i=1|v)v_j]$$
$$\frac{∂L_S}{∂a_i}=\sum _{m=1}^{n_s}[v^m_i−∑_vP(v)v_i]$$
$$\frac {∂L_S}{∂b_i}=\sum _{m=1}^{n_s}[P(h_i=1|v^m)−∑_vP(v)P(h_i=1|v)]$$
到这里就比较明确了,主要就是要求出上面三个梯度;但是因为不好直接求概率分布$P(v)$,前面分析过,计算复杂度非常大,因此采用一些随机采样的方法来得到近似的解。看这三个梯度的第二项实际上都是求期望,而我们知道,样本的均值是随机变量期望的无偏估计。
Gibbs Sampling
吉布斯采样(Gibbs sampling),是MCMC方法的一种。总的来说,Gibbs采样可以从一个复杂概率分布$P(X)$下生成数据,只要我们知道它每一个分量的相对于其他分量的条件概率$P(X_k|X_{−k})$,就可以对其进行采样。而RBM模型的特殊性,隐藏层神经元的状态只受可见层影响(反之亦然),而且同一层神经元之间是相互独立的,那么就可以根据如下方法依次采样:
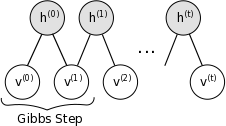
也就是说$hi$是以概率$P(h_i|v_0)$为1,其他的都类似。这样当我们迭代足够次以后,我们就可以得到满足联合概率分布$P(v,h)$下的样本$(v,h)$,其中样本$(v)$可以近似认为是$P(v)$下的样本,下图也说明了这个迭代采样的过程:
有了样本$(v)$就可以求出上面写到的三个梯度$(\frac {∂L_S}{∂w_{ij}},\frac {∂L_S}{∂a_i},\frac{∂L_S}{∂b_i})$了,用梯度上升就可以对参数进行更新了。(实际中,可以在k次迭代以后,得到样本集合${v}$,比如迭代100次取后面一半,带入上面梯度公式的后半部分计算平均值。)
看起来很简单是不是?但是问题是,每一次gibbs采样过程都需要反复迭代很多次以保证马尔科夫链收敛,而这只是一次梯度更新,多次梯度更新需要反复使用gibbs采样,使得算法运行效率非常低。为了加速RBM的训练过程,Hinton等人提出了对比散度(Contrastive Divergence)方法,大大加快了RBM的训练速度。
Contrastive Divergence
我们希望得到$P(v)$分布下的样本,而我们有训练样本,可以认为训练样本就是服从$P(v)$的。因此,就不需要从随机的状态开始gibbs采样,而从训练样本开始。
CD算法大概思路是这样的,从样本集任意一个样本$v^0$开始,经过k次Gibbs采样(实际中k=1往往就足够了),即每一步是:
$$h^{t−1}∼P(h|v^{t−1)}$$
$$v^t∼P(v|h^{t−1})$$
得到样本{v^k}然后对应于三个单样本的梯度,用$v^k$去近似:
$$\frac {∂\ln P(v)}{∂w_{ij}}\approx P(h_i=1|v^0)v^0_j-P(h_i=1|v^k)v^k_j$$
$$\frac {∂\ln P(v)}{∂a_{i}}\approx v^0_i-v^k_i $$
$$\frac {∂\ln P(v)}{∂b_{i}}\approx P(h_i =1| v^0)-P(h_i=1|v^k)$$
上述近似的含义是说,用一个采样出来的样本来近似期望的计算。到这里,我们就可以计算$L_S$的梯度了,上面的CD-k算法是用于在一次梯度更新中计算梯度近似值的。下面给出CD-k的算法执行流程,这里小偷懒一下,就借用截图了[7]。
其中,sample_h_given_v(v,W,a,b),做的事情是这样(sample_v_given_v(h,W,a,b)类似):
记$q_j=P(h_j|v),j=1,2,…,n_h$,产生一个[0,1]的随机数$r_j$,对每一个$h_j$,如果$r_j<q_j$,则$h_j=1$,否则$h_j=0$。
OK, 有了CD-k算法,我们也可以总结RMB整个算法了[7],
参考资料
张春霞,受限波兹曼机简介

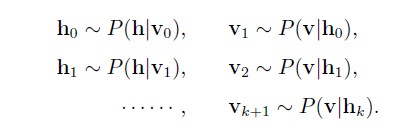


评论